Ajoyib kvadratlar

Afsonalarga koʻra, ajoyib kvadratlar oʻyini qadimgi Xitoyda oʻylab topilgan ekan. Ushbu gʻoyat qiziq matematik oʻyinga bagʻishlangan ilk qoʻlyozma maʼlumotlar esa eramizdan avvalgi 2200-yillarga taalluqli boʻlib, imperator Yu zamonasidagi shunday kvadratlar haqida soʻz yuritadi.

Ajoyib kvadrat N2 sondagi kataklardan iborat boʻlib, kataklarning har biriga boshqasida takrorlanmaydigan butun sonlar yozilgan. Sonlarning kataklarda joylashuv tartibi shunday boʻlishi kerakki, ularni istalgan yoʻnalishda — xoh gorizontal, xoh vertikal va xoh diagonal yoʻnalishda qoʻshib chiqilsa, barcha taraflarda yigʻindi bir xil chiqishi kerak.

Agar ajoyib kvadratdagi barcha butun sonlar toʻplami 1 dan N2 gacha boʻlgan ketma-ketlik qatorini tashkil qilsa, unda ushbu ajoyib kvadrat N tartibli kvadrat deyiladi. Bunday kvadratdagi hamma yoʻnalishda bir xil chiqadigan yigʻindi “sehrli son” deyiladi va u konstant boʻladi. Mazkur “sehrli son” istalgan ajoyib kvadrat uchun doimo N (N2+1) ga teng boʻladi. Uygʻonish davri musavviri boʻlmish Albrext Dyurer 1514-yilda ushbu ajoyib kvadratni tuzib, ommaga namoyish qilgan edi. Uning oʻlchami 4×4 koʻrinishda.

Eʼtibor bersangiz, eng quyi qatordagi ikkinchi va uchinchi kataklardagi (ikkita markaziy katakdagi) sonlar oʻzaro ulab yozilsa “1514” raqami hosil boʻladi, yaʼni musavvir shu tariqa ushbu ajoyib kvadratning hosil qilingan yilini ham kvadratning oʻziga mohirona tarzda muhrlab qoʻygan.

Albrext Dyurerning ushbu ajoyib kvadratida barcha satrlarning ham diagonal, ham gorizontal va vertikal yoʻnalishlar boʻyicha yigʻindisi 34 ga teng chiqadi. Boz ustiga, ushbu ajoyib kvadratning eng chetki, yaʼni burchaklardagi kataklarida joylashgan toʻrtta sonning yigʻindisi ham 34 ga teng chiqishidan tashqari, markazdagi kichik kvadratdagi toʻrtta katakdagi sonlar yigʻindisi ham 34 ga teng chiqadi.

Bu singari ajoyib kvadratlarni chuqur tadqiq qilgan yetuk matematik Bernar Frenikl de Bessi boʻlib, u 1602—1675-yillar orasida Fransiyada yashab oʻtgan. De Bessi toʻrtinchi tartibli ajoyib kvadratlarning boʻlishi mumkin boʻlgan barcha variantlarini aniqlagan va ularning yechimlarini koʻrsatgan.

Toʻrtinchi tartibli ajoyib kvadratlarning jami soni 880 tani tashkil qiladi va ularning barchasi de Bessining oʻlimidan soʻng chop etilgan kitobi — “Ajoyib kvadratlar vaa jadvallar haqida” nomli asarida keltirib oʻtilgan. De Bessi haqli ravishda, bugungi kunda ham “ajoyib kvadratlar qiroli” hisoblanadi.

Odamzod 3×3 oʻlchamdagi eng sodda, ajoyib kvadratlarni oʻylab topganidan beri ancha muddat oʻtdi. Qizigʻi shundaki, 3×3 oʻlchamdagi eng sodda, ajoyib kvadratlar bir qarashda bir-biri bilan umuman aloqada boʻlmagan, oʻzaro yot sivilizatsiyalarda ham qadimdan maʼlum boʻlgan. Xususan, shunday ajoyib kvadratlar mayya hindularida ham, Afrikadagi Xasus qabilasida ham, Janubiy-sharqiy Osiyo changalzorlarida yashagan xalqlarda ham boʻlgan. Hozirda matematiklar yuqori oʻlchamdagi fazoviy jismlar sirtidagi ajoyib kvadratlarning xossalarini oʻrganmoqda. Xususan, toʻrt oʻlchamli giperkub boʻylab, barcha yoʻnalishlarda teng yigʻindi keltirib chiqaruvchi ajoyib kvadratlar oʻrganilmoqda.

Rasmda: Barselonadagi nasroniylar ibodatxonasida 4×4 oʻlchamdagi ajoyib kvadrat tasviri tushirilgan boʻlib, u barcha yoʻnalishlar boʻyicha yigʻindi 33 raqamini beradi. Ularning eʼtiqodiga koʻra, ushbu raqam Iso Masihning samoga koʻtarilgan paytidagi yoshini ifodalar emish. Lekin ushbu kvadratni asl ajoyib kvadrat deyish ham toʻgʻri emas. Chunki bunda shart bajarilmayapti, yaʼni kvadrat ichidagi kataklarda baʼzi sonlar takrorlanmoqda.

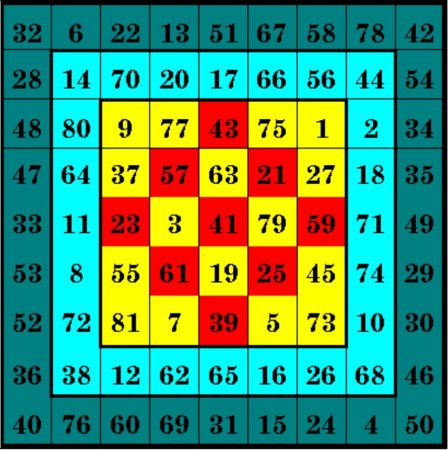
Ajoyib kvadratlar haqida gap ketganda, Jon Xendrik tuzgan eng murakkab va shu bilan birga, eng mukammal ajoyib kombinatsion kvadratni ham esga olib oʻtish shart. Jon Xendrik ajoyib kvadrati 9-tartibli ajoyib kvadrat boʻlib, unda 1 dan 81 gacha boʻlgan sonlar ishtirok etadi. Unda hamma yoʻnalishlar yigʻindi boʻyicha 369 raqamiga teng boʻlib chiqadi. Shu bilan birga, ushbu kvadrat ichida yana uchta boshqa ajoyib kvadratlar ham shunday mohirona joylanganki, ularning oʻzida ham 287, 205 va 123 sonlari chiqadi. Ushbu ichki ajoyib kvadratlar moviy, sariq va qizil ranglar bilan alohida yaqqol koʻrsatilgan. Qizil rangli, yaʼni 3-tartibli markaziy, ichki ajoyib kvadrat 45° ga burilgan holda tasvirlangan.